Resultant Amplitude In Shm

Find i amplitude of resultant SHM. Consider two SHMs having same period and parallel to each other where a1 and a2 are amplitudes of two SHMs respectively.

Three Simple Harmonic Motions Of Equal Amplitudes A And Equal Time Periods In The Same Direction Youtube

In such a case the resultant motion of the body depends on the periods paths and the relative phase angles of the different SHMs to which it is subjected.

Resultant amplitude in shm. The amplitude of the resultant SHM is 143 c When the phase difference between the two component SHMs is It 2 y-axis 2A2 x-axis 2A1 Figure 5. Units and is a constant. When the two SHMs add their respective displacement vectors add up according to.

A2A i think there is a little inaccuracy in the book a better way would have to use displacement vectors of the respective SHMs in place of amplitude in the diagram. The amplitude and phase of the resultant SHM depends on the amplitudes of the two individual SHMs as well as the phase difference between them. Then the resultant motion is which shows that the resultant motion is SHM with the same angular frequency and an amplitude equal to the difference of the amplitude of the two motions.

A the amplitude maximum displacement in m t the time since the oscillation began in s. Ii equation of the resultant SHM. Thus we can see that the resultant motion is also SHM with the same frequency as the component motions.

Of the same angular frequency hence the same period but of amplitude R and initial phase . The extra terms in this equation are. It shows that the combination superposition of two linear SHMs of the same period and occurring along the same path is also an SHM.

A At t and 0 Al sin 0 x2 142 sin OSCILLATIONS AND WAVES o Thus the resultant displacement at t 0 is. In such a case the resultant motion of the body depends on the periods paths and the relative phase angles of the different SHMs to which it is subjected. 1 0 x A sin t 2 0 4 2 4 x A sin t 3 0 2 x A cos t 4 0 5 37 x A sin t A 0 9 A A B 1 1 3 tan C 0 3 A A D 1 1 9 tan 2.

Time Period and Frequency of SHM. A1 anda2 are initial phase angle of two SHMs respectively whose displacements are given by. If playback doesnt begin shortly try restarting your device.

In figure we indicate for d p the different motion considered and their rotating vectors. The key features of SHM are that the motion is repetitive or periodic and that it involves a maximum displacement from the position of equilibrium. Amplitude in SHM It is the maximum displacement of the particle from the mean position.

Velocity we can calculate the velocity of the object at any point in its oscillation using the equation below. These features must appear in any mathematical representation of SHM. So the equation of the resultant is x 1 x 2 x 3 A sin t sin t 3 sin t 3 2 adding the first term sin t and third term sin t 3 2 using trigonometric formula sin A sin B 2 sin 2 A B cos 2 A B we have.

Period and amplitude in SHM circular motion and the equations of SHM Equations 1411 and 1412 show that the period and frequency of simple harmonic motion are completely determined by the mass m and the force constant k. X_1 5sin omega t x_2 5 sin omega t 53 x_3 - 10 cos omega t. The minimum time after which the particle keeps on repeating its motion is known as the time period or the shortest time taken to complete one oscillation is also defined as the time period.

Find the amplitude in SI. The magnitude of the maximum displacement from equilibrium is called the amplitude A of the motion. Resultant amplitude is R sqrtR sin2 R cos2.

Find resultant amplitude A and phase constant in case of superposition of the following SHMs along X-axis. The elliptical path traced by the resultant motion of the particle when the phase. Find the resultant amplitude of the following simple harmonic equations.

If two SHMs of different amplitudes A and B are superimposed with each other then the amplitude of the resultant SHM is given by R A 2 B 2 2 A B c o s . That is For that reason we say that the motions are in opposition. is the phase difference between the SHMs The resultant amplitude will be maximum if the phase difference between them is 0 or 2 The correct option is d.

Equation 7 is the equation of an SHM. The resultant amplitude due to superposition of three simple harmonic motion x1 3 sin t The resultant amplitude due to superposition of three simple harmonic motion x1 3 sin t x2 5 sin t 37 and x3 -15 cos t is. The mass and diameter of a planet are twice those of earth.

A particle is subjected to two simple harmonic motions. A1 anda2 are initial phase angle of two SHMs respectively whose displacements are given by. Please log in or register to add a comment.

Units of resultant SHM of a particle in xy plane due to superposition of SHMs x 3sin t and y 4 sint where x y and t are in SI. The terms in this equation are the same as the equations above. The resultant amplitude due to superposition of three simple harmonic motions x_ 1 3sin omeg.

Consider two SHMs having same period and parallel to each other where a1 and a2 are amplitudes of two SHMs respectively. A uniform disc of radius 5 cm and mass 200 g is fixed at its centre to a metal wire the other end of which is fixed to a ceiling.

Determine Resultant Amplitude After Super Position Of Given Four Waves With Hel Youtube

Can The Amplitude Of An Shm Be Time Dependent Why Or Why Not Quora

Three Simple Harmonic Motion Of Equal Amplitudes A And Equal Time Periods In The Same Directio Youtube

The Resultant Amplitude When Two Waves Of Two Waves Of Same Frequency But With Youtube

When Two Simple Harmonic Motions Of Same Periods Same Amplitude Having Phase Difference Of 3pi 2 And At Right Angles To Each Other Are Super Imposed The Resultant Wave From Is A

A Particle Is Subjected To Two Simple Harmonic Motion In The Same Direction Having Equal Amplitudes And Equal Frequency If The Resultant Amplitude Is Equal To The Amplitude Of The Individual Motions

If Two Shms Of Different Amplitudes Are Added Together The Resultant Shm Will Be A Maximum If The Phase Difference Between Them Is

Find The Amplitude Of The Simple Harmonic Motion Obtasined By Combining The Motions X 1 2 0 Cm Sinomegat And X 2 2 0cm Sin Omegat Pi 3

The Resultant Of Two Rechangular Simple Harmonic Motion Of The Same Frequency And Unequal Amplitude Youtube

Two Particle Execute Shm Of Same Amplitude Of 20 Cm With Same Period Along The Same Line About The Same Equilibrium Position The Maximum Distance Between The Two Is 20 Cm Their

The Resultant Amplitude Of A Vibrating Particle By The Superposition Of The Youtube

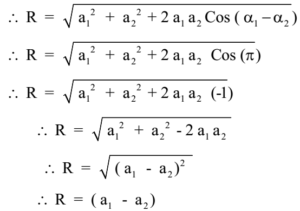
Composition Of Two Shm Expression For Resultant Shm Amplitude

Resultant Amplitude And Intensity Myrank

Two Particles Are In Shm In A Straight Line About Same Equilibrium Position Amplitude A And Youtube

Find The Amplitude And Initial Phase Of A Partical In Shm Whose Motion Equation Is Given As Y Youtube

Composition Of Two Shm Expression For Resultant Shm Amplitude

Simple Harmonic Motion Formulas 2 Mathematics Motion Physics Physics

The Resultant Amplitude Due To Superposition Of Three Simple Harmonic Motions X 1 3sin Omeg Youtube

Basic Concepts On Displacement Position And Displacement Time Graph Physics And Mathematics Basic Concepts Physics Lessons